btvector

发表于 2025-05-10 分类于 Bustub Disqus： 0 Comments 本文字数： 8.8k 阅读时长 ≈ 32 分钟

这是一个基于BusTub实现向量拓展的教程，支持向量数据类型以及相关的优化。根据这篇博客实现，具体流程如下：
请添加图片描述

向量数据库介绍

向量就可以理解为c++中的vector，比如[1, 2, 3]。

而原版的Bustub（或者传统关系型数据库）会有多种数据类型，比如int，float，varchar….

而向量数据库就是对其新增加一个数据类型，vector。

例如，在支持向量类型的数据库中，可以这样定义和插入数据：

create table embeddings (
    id primary key,
    embedding vector(3)
);

insert into embeddings (embedding) values ('[1.0, 2.0, 3.0]');

这就建立一个vector数据类型embedding，embedding 是一列，类型为 vector(3)，表示一个包含 3 个浮点数的向量。可以往里插入值 **[1.0, 2.0, 3.0]**。

如果使用传统的关系型数据库 schema，通常需要这样展开成多列：

create table embeddings (
    id primary key,
    v1 float,
    v2 float,
    v3 float
);

insert into embeddings values (1.0, 2.0, 3.0);

换句话说，向量数据类型就是把原本的三个float数据类型的列合并封装成一个数据类型vector整体。

乍一看这貌似没啥特别的，不就新增一个数据类型吗？，三列还是一列似乎区别不大，用得把整个数据库都改名成”向量“数据库吗？

而事实不止于此，向量数据库的核心是，对向量这个数据类型相关的操作进行大量的优化，极大提升向量操作的效率。

比如：

统一的向量数据模型：向量作为一个整体存储和管理，支持高维数据。
高效的向量运算：原生支持向量间的相似度计算（L2距离、余弦相似度、内积等）。
专用的向量索引结构：如 IVFFlat、HNSW、DiskANN 等，使得向量检索在百万到亿级规模的数据中依然可以快速响应。
更好的存储布局：连续内存存储向量，提高了访问局部性和 CPU cache 命中率。

不仅是新增了一个vector数据类型，更是从数据组织、查询优化、索引加速等各个方面，为处理大规模高维向量数据进行了深度定制。

随着机器学习、推荐系统、检索系统的发展，对高效向量检索的需求不断增加，向量数据库已经成为支撑这些应用的重要基础设施。

一句话总结： 向量数据库就是支持vector数据类型，并在此基础上对vector类型相关操作进行极大的优化。

所以让bustub支持向量化思路也很清晰了，先支持新的向量数据库类型（这个容易），再一步步对有关向量的操作进行优化。

环境配置

教程建议clone新的repo，但我是直接基于我之前完成的四个project，截止目前这个分支只有七个新commit，所以建议直接一个个commit用 git cherry-pick来一步步同步，这样也可以清楚新增加了哪些东西。

本地增加对方为远程repo：

1	git remote add vectordb git@github.com:skyzh/bustub-vectordb.git

然后拉远程库的分支

1	git fetch vectordb

然后即可看到对方分支

1	git branch -r

查看你想合并的分支（main）

1	git checkout -b merge-vectordb vectordb/main

这会在本地建立一个分支merge-vectordb，指向 vectordb/vectorized。

本地新建一个专门用来实现矢量化的分支

1	git switch -c feature/vectordb

然后就可以一步步用cherry-pick合并，在本地或者github都可以找到fork之后的七个新commit，github上看会清晰很多，比如合并第一个message为“stub code for bpm and table heap”的commit：

1	git cherry-pick cc270104687b2f673f26c9490642140ef0fe491f

然后根据自己的实现解决conflict再合并下一个即可。最后git graph类似：
请添加图片描述
main/origin 就是我合并前，feature/vector-db就是我合并后的。

然后就可以编译运行：

1
2
3

cmake -B build
cd build
make -j10 shell sqllogictest

编译了bustub shell, 就可以运行创建向量命令了：

1	./bin/bustub-shell

❯ ./bin/bustub-shell
Welcome to the BusTub shell! Type \help to learn more.

bustub> select array [1.0, 2.0, 3.0];
+-------------+
| __unnamed#0 |
+-------------+
| [1,2,3]     |
+-------------+
bustub>

Insertion & Sequential Scan

vector_expression.h中补齐几个基本的向量运算：

inline auto InnerProduct(const std::vector<double> &left, const std::vector<double> &right) -> double {
  double ip = 0.0;
  for (size_t i = 0; i < left.size(); ++i) {
    ip += left[i] * right[i];
  }
  return ip;
}

inline auto VectorNorm(const std::vector<double> &v) -> double {
  double norm = 0.0;
  for (double x : v) {
    norm += std::pow(x, 2);
  }
  return std::pow(norm, 0.5);
}

inline auto ClampNearZero(double number) -> double {
  return std::abs(number) < 1e-8 ? 0.0 : number;
}

inline auto ComputeDistance(const std::vector<double> &left, const std::vector<double> &right,
                            VectorExpressionType dist_fn) {
  auto sz = left.size();
  BUSTUB_ASSERT(sz == right.size(), "vector length mismatched!");
  switch (dist_fn) {
    case VectorExpressionType::L2Dist: {
      double l2d = 0.0;
      for (size_t i = 0; i < sz; ++i) {
        l2d += std::pow(left[i] - right[i], 2);
      }
      return ClampNearZero(std::pow(l2d, 0.5));
    }
    case VectorExpressionType::InnerProduct: {
      return ClampNearZero(- InnerProduct(left, right));
    }
    case VectorExpressionType::CosineSimilarity: {
      double norm_left = VectorNorm(left);
      double norm_right = VectorNorm(right);
      if (norm_left == 0 || norm_right == 0) {
        // One of the vectors is zero vector.
        return 1.0;
      }
      return ClampNearZero(1.0 - InnerProduct(left, right) / (norm_left * norm_right));
    }
    default:
      BUSTUB_ASSERT(false, "Unsupported vector expr type.");
  }
}

只要merge正确，那么此时你之前实现的insertion_executor和seq_scan_executor都可以使用。运行

1	./bin/bustub-sqllogictest ../test/sql/vector.01-insert-scan.slt --verbose

即可通过测试。

而这里新增了一个Vector_Index_Scan_Executor, 就是利用向量索引进行扫描的执行器，应该是已经帮你实现好了，只不过不支持MVCC。

Naive K-Nearest Neighbors

且看这句sql：

1 2	CREATE TABLE t1(v1 VECTOR(3), v2 integer); SELECT v1 FROM t1 ORDER BY ARRAY [1.0, 1.0, 1.0] <-> v1 LIMIT 3;

这就是试图寻找表t1中距离ARRAY [1.0, 1.0, 1.0] 最近的三个vector。

Naive KNN 在向量数据库里指的是一种最基础的最近邻搜索方法，特点是：

遍历所有数据点（Brute Force）
计算查询向量到每个数据点的距离
取距离最近的前K个

也就是说，不管数据库里有多少个向量，每次查询都会全量扫描一遍。

由于之前实现过sort，limit，topN，这里仍然不需要任何更改，直接可以通过测试。(怎么感觉啥也没干。。。）

1 2	make -j8 sqllogictest ./bin/bustub-sqllogictest ../test/sql/vector.02-naive-knn.slt --verbose

Matching the Plan Structure

正如我最开始将的逻辑，先支持了向量数据类型的操作，紧接着就是对其相关操作进行优化了。

如果数据库里有几百万、上亿个向量，你想找“跟查询向量最接近的K个”，每次都暴力扫一遍所有向量，就会非常慢。这时候，就需要一种特殊的索引结构，能对向量距离计算极大加速。

Vector Index Scan Plan 介绍

接下来实现对vector进行索引扫描，实现一个新的优化器规则，将seq_scan优化成Vector Index Scan。

需要的结果大概是：

EXPLAIN (o) SELECT v1 FROM t1 ORDER BY ARRAY [1.0, 1.0, 1.0] <-> v1 LIMIT 2;
=== OPTIMIZER ===
TopN { n=2, order_bys=[("Default", "l2_dist([1.000000,1.000000,1.000000], #0.0)")]}
  Projection { exprs=["#0.0"] }
    SeqScan { table=t1 }

优化后：

EXPLAIN (o) SELECT v1 FROM t1 ORDER BY ARRAY [1.0, 1.0, 1.0] <-> v1 LIMIT 2;
=== OPTIMIZER ===
Projection { exprs=["#0.0"] }
  VectorIndexScan { index_oid=1, index_name=t1v1hnsw, table_oid=24, table_name=t1
  base_vector=[1.000000,1.000000,1.000000], limit=2 }

即将TopN节点和SeqScan节点合并成VectorIndexScan节点。利用TopN中的距离函数走对应索引，直接扫描两个tuple即可而不用全表扫描，极大提升效率。

但TopN和SeqScan不一定是挨着的，这俩节点之间的位置有三种基本情况：

Case 1：TopN和SeqScan紧挨着

1 2	TopN { n=2, order_bys=[("Default", "l2_dist([1.000000,1.000000,1.000000], #0.0)")]} SeqScan { table=t1 }

最简单的情况。

Case 2: TopN紧接着一个Projection

1
2
3

TopN { n=2, order_bys=[("Default", "l2_dist([1.000000,1.000000,1.000000], #0.0)")]}
  Projection { exprs=["#0.0", "l2_dist([1.000000,1.000000,1.000000], #0.0)"] }
    SeqScan { table=t1 }

Case 3：TopN紧接着一个Projection且其改变了列的顺序

1
2
3

TopN { n=2, order_bys=[("Default", "l2_dist([1.000000,1.000000,1.000000], #0.1)")]}
  Projection { exprs=["#0.1", "#0.0"] }
    SeqScan { table=t1 }

总而言之，就是遇到这样的结构就可以尝试优化成VectorIndexScan：

   TopN
    |
Projection (optional)
    |
 seq_scan

因为之前实现了 Predicate Pushdown 和 合并filter&SeqScan，所以应该没有遗漏情况。

于是逻辑就很清晰了，跟之前Project3部分的差不多，从上往下遍历PlanTree，直到遇到TopN - Projection（可有可无）- seq_scan 的节点子树即可尝试优化。

从TopN的order_bys条件中提取向量距离表达式（比如l2_dist)。从TopN中获取向量在tuple中的col_idx, 如果经过projection节点，检查其是否改变了col_idx。

Vector Index Scan Plan 优化实现

绝大部分只需改动 vector_index_scan.cpp。

先实现一个helper function，用于寻找匹配的vector index。其可根据条件，搜索一个table是否有可以使用的vector index，有的话返回index，否则返回nullptr。

/**
 * @brief Match vector_index of a table by col_idx, VectorExpressionType and vector_index_match_method.
 *
 * @param dist_fn {L2Dist, InnerProduct, CosineSimilarity}
 * @param vector_index_match_method 
 * - unset or empty: match the first vector index available.
 * - hnsw: only match the HNSW index.
 * - ivfflat: only match the IVFFlat index.
 * - none: do not match any index and do exact nearest-neighbor search.
 */
auto MatchVectorIndex(const Catalog &catalog, table_oid_t table_oid, uint32_t col_idx, VectorExpressionType dist_fn,
                      const std::string &vector_index_match_method) -> const IndexInfo * {
  if (vector_index_match_method == "none") {
    return nullptr;
  }

  const auto table_info_ptr = catalog.GetTable(table_oid);
  if (table_info_ptr == nullptr) {
    return nullptr;
  }
  auto index_infos = catalog.GetTableIndexes(table_info_ptr->name_);
  
  for (const auto idx_info : index_infos) {
    if (idx_info == nullptr) {
      continue;
    }
    // Key has only one column, and should be col_idx.
    if (idx_info->index_->GetIndexColumnCount() != 1 || idx_info->index_->GetKeyAttrs()[0] != col_idx) {
      continue;
    }

    const auto vector_index = dynamic_cast<VectorIndex *>(idx_info->index_.get());
    if (vector_index != nullptr && vector_index->distance_fn_ == dist_fn) {
      if (vector_index_match_method.empty() || vector_index_match_method == "unset") {
        return idx_info;
      }
      if (vector_index_match_method == "hnsw" && dynamic_cast<const HNSWIndex *>(vector_index) != nullptr) {
        return idx_info; 
      }
      if (vector_index_match_method == "ivfflat" && dynamic_cast<const IVFFlatIndex *>(vector_index) != nullptr) {
        return idx_info;
      }
    }
  }

  return nullptr;
}

然后先实现 Case1 的情况，即 TopN - SeqScan

auto Optimizer::OptimizeAsVectorIndexScan(const AbstractPlanNodeRef &plan) -> AbstractPlanNodeRef {
  std::vector<AbstractPlanNodeRef> children;
  for (const auto &child : plan->GetChildren()) {
    children.emplace_back(OptimizeAsVectorIndexScan(child));
  }
  auto optimized_plan = plan->CloneWithChildren(std::move(children));

  // Encounter structure like:
  //    TopN
  //     |
  // Projection (optional)
  //     |
  //  seq_scan 
  //
  // It can be optimized to VectorINdexScan.

  if (optimized_plan->GetType() != PlanType::TopN) {
    return optimized_plan;  // Not TopN, directly return.
  }

  auto topn_plan = dynamic_cast<TopNPlanNode &>(*optimized_plan);
  auto order_bys = topn_plan.GetOrderBy();
  if (order_bys.size() != 1) {
    return optimized_plan;  // todo: Now, only care about one order_by.
  }

  VectorExpressionType vector_expr_type = VectorExpressionType::UnKnown;
  std::shared_ptr<const ArrayExpression> base_vector;
  uint32_t col_idx = -1U;
  if (!ExtractVectorScanParams(order_bys[0], vector_expr_type, base_vector, col_idx)) {
    return optimized_plan;  // Not valid vector expression.
  }

  // auto &pre_plan = topn_plan;
  auto cur_plan = topn_plan.GetChildPlan();

  // Projection layer.
  if (cur_plan->GetType() == PlanType::Projection) {
    return optimized_plan; // todo: 
  }

  // Seq_scan layer.
  if (cur_plan->GetType() == PlanType::SeqScan) {
    auto &seq_scan_plan = dynamic_cast<const SeqScanPlanNode &>(*cur_plan);
    const auto index_info = MatchVectorIndex(catalog_, seq_scan_plan.GetTableOid(), col_idx, vector_expr_type, vector_index_match_method_);
	if (index_info == nullptr) {
	  return optimized_plan;
  	}
    auto vector_indexscan_plan = std::make_shared<VectorIndexScanPlanNode>(topn_plan.output_schema_, 
      seq_scan_plan.GetTableOid(), seq_scan_plan.table_name_, index_info->index_oid_, 
      index_info->index_->GetName(), base_vector,topn_plan.GetN());
    return vector_indexscan_plan;
  }

  return optimized_plan;
}

可以看到我目前只考虑了最简单的情况，即TopN中的order_bys只有一个pair。也不考虑prediction。

我把从一个order_by对中提取构造信息的功能封装成单独的函数:

static auto ExtractVectorScanParams(const std::pair<OrderByType, AbstractExpressionRef> &order_by, 
                                    VectorExpressionType &vector_expr_type,
                                    std::shared_ptr<const ArrayExpression> &base_vector, 
                                    uint32_t &col_idx) -> bool {
  if (order_by.first != OrderByType::DEFAULT && order_by.first != OrderByType::ASC) {
    return false;  // vector index scan does not support descending order.
  }

  const auto vector_expr = dynamic_cast<const VectorExpression *>(order_by.second.get());
  if (vector_expr == nullptr) {
    return false;
  }

  vector_expr_type = vector_expr->expr_type_;

  auto left = dynamic_cast<const ArrayExpression *>(vector_expr->GetChildAt(0).get());
  auto left_col_expr = dynamic_cast<const ColumnValueExpression *>(vector_expr->GetChildAt(0).get());
  auto right = dynamic_cast<const ArrayExpression *>(vector_expr->GetChildAt(1).get());
  auto right_col_expr = dynamic_cast<const ColumnValueExpression *>(vector_expr->GetChildAt(1).get());

  if (left != nullptr && right_col_expr != nullptr) {
    base_vector = std::dynamic_pointer_cast<const ArrayExpression>(
      std::shared_ptr<AbstractExpression>(left->CloneWithChildren(left->GetChildren()))
    );
    col_idx = right_col_expr->GetColIdx();
  } else if (right != nullptr && left_col_expr != nullptr) {
    base_vector = std::dynamic_pointer_cast<const ArrayExpression>(
      std::shared_ptr<AbstractExpression>(right->CloneWithChildren(right->GetChildren()))
    );
    col_idx = left_col_expr->GetColIdx();
  } else {
    return false;
  }

  return true;
}

此时，即可对Case1 情况进行优化。

<main>:13
EXPLAIN (o) SELECT * FROM t1 ORDER BY ARRAY [1.0, 1.0, 1.0] <-> v1 LIMIT 2;
----
=== OPTIMIZER ===
VectorIndexScan { index_oid=1, index_name=t1v1hnsw, table_oid=24, table_name=t1
base_vector=[1.000000,1.000000,1.000000], limit=2 }

接下来实现Case2，在我已经留下的位置补上Projection相关操作即可：

... ...

  AbstractPlanNodeRef projection_node = nullptr;
  auto cur_plan = topn_plan.GetChildPlan();

  // Projection layer.
  if (cur_plan->GetType() == PlanType::Projection) {
    auto projection_plan = dynamic_cast<const ProjectionPlanNode *>(cur_plan.get());
    projection_node = cur_plan;
    cur_plan = projection_plan->GetChildPlan();
  }

... ...

	if (projection_node != nullptr) {
      return projection_node->CloneWithChildren({vector_indexscan_plan});
    }
    return vector_indexscan_plan;

... ...

即可优化Case2的情况：

<main>:10
EXPLAIN (o) SELECT v1 FROM t1 ORDER BY ARRAY [1.0, 1.0, 1.0] <-> v1 LIMIT 2;
----
=== OPTIMIZER ===
Projection { exprs=["#0.0"] }
  VectorIndexScan { index_oid=1, index_name=t1v1hnsw, table_oid=24, table_name=t1 base_vector=[1.000000,1.000000,1.000000], limit=2 }

<main>:16
EXPLAIN (o) SELECT v1, ARRAY [1.0, 1.0, 1.0] <-> v1 FROM t1 ORDER BY ARRAY [1.0, 1.0, 1.0] <-> v1 LIMIT 2;
----
=== OPTIMIZER ===
Projection { exprs=["#0.0", "l2_dist([1.000000,1.000000,1.000000], #0.0)"] }
  VectorIndexScan { index_oid=1, index_name=t1v1hnsw, table_oid=24, table_name=t1 base_vector=[1.000000,1.000000,1.000000], limit=2 }

而最难的case3：

<main>:19
EXPLAIN (o) SELECT v2, v1 FROM t1 ORDER BY ARRAY [1.0, 1.0, 1.0] <-> v1 LIMIT 2;
----
=== OPTIMIZER ===
TopN { n=2, order_bys=[("Default", "l2_dist([1.000000,1.000000,1.000000], #0.1)")]}
  Projection { exprs=["#0.1", "#0.0"] }
    SeqScan { table=t1 }

目前无法优化。

因为可以看到，从TopN中可以锁定col_idx为1，而Projection节点重新映射col_idx成0，所以在seq_scan中实际需要寻找的是col_idx=0对应列的索引，而根据我目前的实现，仍然找的是col_idx=1对应的索引。而col_idx=1的列根本不是Vector，所以MatchVectorIndex 函数自然找不到匹配的索引，所以就会返回nullptr而无法优化。

所以我们要做的就是在 Projection layer 中查看是否需要重新映射col_idx。

// Projection layer.
if (cur_plan->GetType() == PlanType::Projection) {
  projection_node = cur_plan;
  auto projection_plan = dynamic_cast<const ProjectionPlanNode *>(cur_plan.get());
  cur_plan = projection_plan->GetChildPlan();

  // Re-map col_idx.
  BUSTUB_ASSERT(col_idx < projection_plan->GetExpressions().size(), "col_idx greater than projection.");
  auto col_proj_expr = projection_plan->GetExpressions()[col_idx];
  auto col_column_value_expr = dynamic_cast<ColumnValueExpression *>(col_proj_expr.get());
  if (col_column_value_expr == nullptr) {
    return optimized_plan;  // Not direct projecting expression, do not support optimizing.
  }
  col_idx = col_column_value_expr->GetColIdx();
}

增加re-map后，即可通过所有测试：

1	/bin/bustub-sqllogictest ../test/sql/vector.03-index-selection.slt --verbose

Bonus

这个部分的bonus也很容易实现，

EXPLAIN (o) SELECT * FROM (SELECT v1, ARRAY [1.0, 1.0, 1.0] <-> v1 as distance FROM t1) ORDER BY distance LIMIT 2;

TopN { n=2, order_bys=[("Default", "#0.1")]}
  Projection { exprs=["#0.0", "l2_dist([1.000000,1.000000,1.000000], #0.0)"] }
    SeqScan { table=t1 }

目前无法得到优化。因为我目前只在TopN中找满足条件的Vector Expression，但这个sql语句中vector expression 放在了Projection中，所以只需要在上面代码 projection layer 加入寻找vector expression的功能即可。

再拆出一层封装函数：

static auto ExtractVectorScanFromOrderBy(const std::pair<OrderByType, AbstractExpressionRef> &order_by, 
                                        VectorExpressionType &vector_expr_type,
                                        std::shared_ptr<const ArrayExpression> &base_vector, 
                                        uint32_t &col_idx) -> bool {
  if (order_by.first != OrderByType::DEFAULT && order_by.first != OrderByType::ASC) {
    return false;  // vector index scan does not support descending order.
  }

  return ExtractVectorScanFromAbsExpr(order_by.second, vector_expr_type, base_vector, col_idx);
}

static auto ExtractVectorScanFromAbsExpr(const AbstractExpressionRef &expr, VectorExpressionType &vector_expr_type,
                                         std::shared_ptr<const ArrayExpression> &base_vector, 
                                         uint32_t &col_idx) -> bool {
  const auto vector_expr = dynamic_cast<const VectorExpression *>(expr.get());
  if (vector_expr == nullptr) {
    return false;
  }

  vector_expr_type = vector_expr->expr_type_;

  auto left = dynamic_cast<const ArrayExpression *>(vector_expr->GetChildAt(0).get());
  auto left_col_expr = dynamic_cast<const ColumnValueExpression *>(vector_expr->GetChildAt(0).get());
  auto right = dynamic_cast<const ArrayExpression *>(vector_expr->GetChildAt(1).get());
  auto right_col_expr = dynamic_cast<const ColumnValueExpression *>(vector_expr->GetChildAt(1).get());

  if (left != nullptr && right_col_expr != nullptr) {
    base_vector = std::dynamic_pointer_cast<const ArrayExpression>(
      std::shared_ptr<AbstractExpression>(left->CloneWithChildren(left->GetChildren()))
    );
    col_idx = right_col_expr->GetColIdx();
  } else if (right != nullptr && left_col_expr != nullptr) {
    base_vector = std::dynamic_pointer_cast<const ArrayExpression>(
      std::shared_ptr<AbstractExpression>(right->CloneWithChildren(right->GetChildren()))
    );
    col_idx = left_col_expr->GetColIdx();
  } else {
    return false;
  }

  return true;
}

增加并修改Projection Layer代码：

... ...
  // Projection layer.
  if (cur_plan->GetType() == PlanType::Projection) {
    projection_node = cur_plan;
    auto projection_plan = dynamic_cast<const ProjectionPlanNode *>(cur_plan.get());
    cur_plan = projection_plan->GetChildPlan();

    auto proj_exprs = projection_plan->GetExpressions();

    if (col_idx == -1U) {
      // Did not find vector expression in TopN, search it in projection.
      for (const auto &expr : proj_exprs) {
        auto ve = dynamic_cast<VectorExpression *>(expr.get());
        if (ve != nullptr && !ExtractVectorScanFromAbsExpr(expr, vector_expr_type, base_vector, col_idx)) {
          break;
        }
      }
    } else {
      // Re-map col_idx.
      BUSTUB_ASSERT(col_idx < projection_plan->GetExpressions().size(), "col_idx greater than projection.");
      auto col_proj_expr = proj_exprs[col_idx];
      auto col_column_value_expr = dynamic_cast<ColumnValueExpression *>(col_proj_expr.get());
      if (col_column_value_expr == nullptr) {
        return optimized_plan;  // Not direct projecting expression, do not support optimizing.
      }
      col_idx = col_column_value_expr->GetColIdx();
    }
  }

  if (col_idx == -1U) {
    return optimized_plan;  // Did not find vector expr in both TopN and Projection.
  }

... ...

在测试文件最下面增加语句：

statement ok
set vector_index_method=unset

statement ok
EXPLAIN (o) SELECT * FROM (SELECT v1, ARRAY [1.0, 1.0, 1.0] <-> v1 as distance FROM t1) ORDER BY distance LIMIT 2;

运行可看到，成功优化Bonus：

<main>:43
EXPLAIN (o) SELECT * FROM (SELECT v1, ARRAY [1.0, 1.0, 1.0] <-> v1 as distance FROM t1) ORDER BY distance LIMIT 2;
----
=== OPTIMIZER ===
Projection { exprs=["#0.0", "l2_dist([1.000000,1.000000,1.000000], #0.0)"] }
  VectorIndexScan { index_oid=1, index_name=t1v1hnsw, table_oid=24, table_name=t1 base_vector=[1.000000,1.000000,1.000000], limit=2 }

目前就实现了在优化器中将seq_scan优化成VectorIndexScan，后续就可实现向量索引的具体算法了。经过前面Project 3 Leaderboard部分的锤炼，这部分实现新的优化器规则还是毫无压力的，但给的测试也实在不全面，我目前也没检查edge cases，遇到问题再改吧，但更改后不一定会贴出来了。

Inverted File Flat Index

现在实现了优化器中将 PlanTreeNode 优化成利用向量索引扫描的 VectorIndexScan，从这里开始，我们就要开始实现向量索引的具体算法，实现对向量距离操作的加速优化。

这一部分，是实现Inverted File Flat Index。

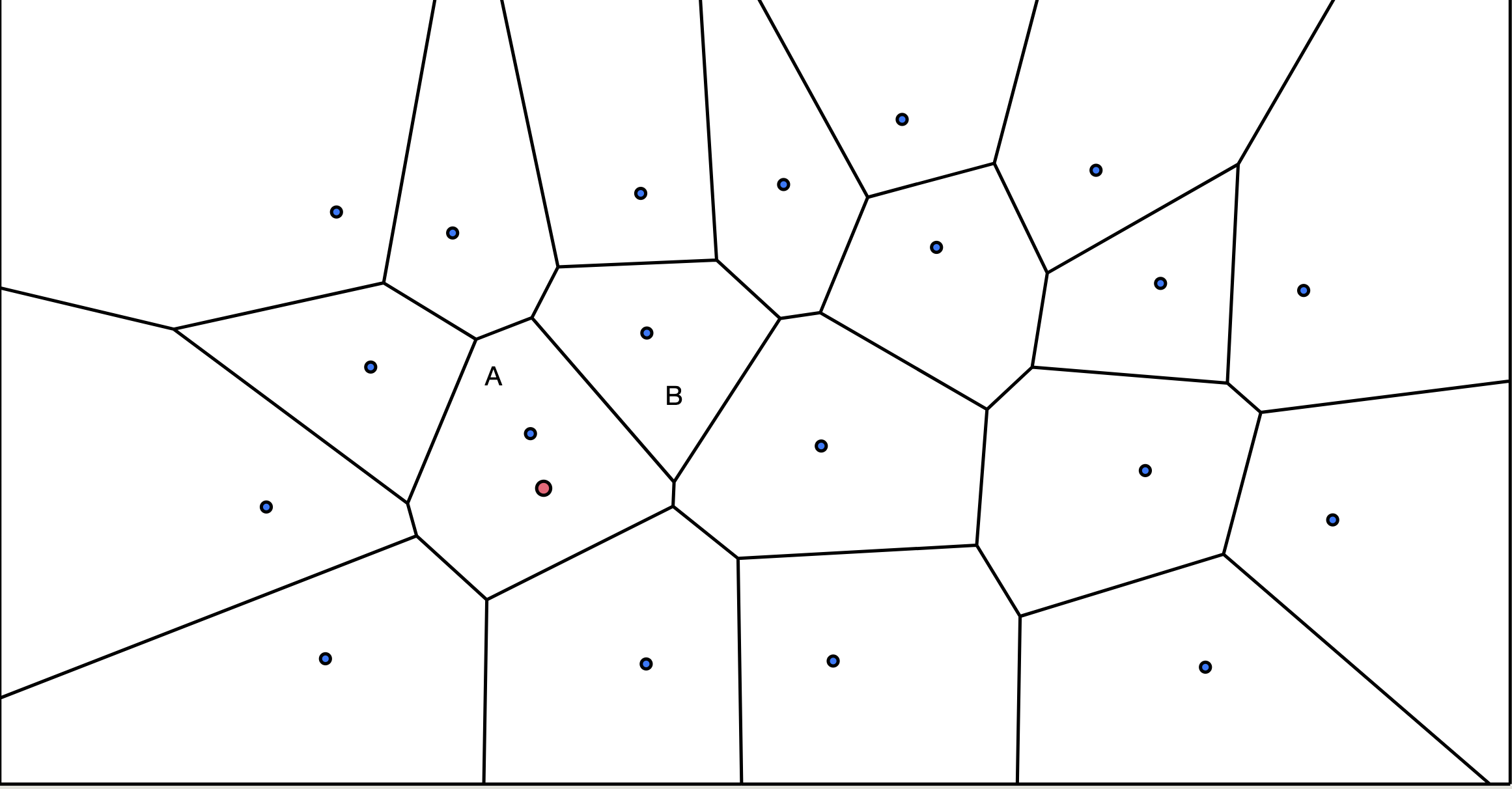
思路

IVFFlat 的基本思路是：先使用聚类（如 K-means）将数据点划分为多个cluster，每个cluster由其“质心”代表。这样，向量空间被划分成多个以cluster质心为界的格子。插入新数据时，只需将它归入其所在格子的簇中。查询时，只在距离查询向量最近的几个cluster中进行精确搜索，跳过大量无关向量，从而在牺牲部分精度的同时，大幅提高搜索效率。

这也是一种轻量级的向量索引，构建快，占用内存少，但是查找精度不足。

格子边界就是两个相邻“质心”连线的垂直平分线，即保证边界线上的点到左右两个格子质心距离都相等，有点像固体物理的晶格。并且因为开销过大，每个格子的质心是不会随着数据插入而动态调整的，只会在构建时就确定。这也是该算法的缺点之一。同时因为查找最近邻几个cluster，所以查找精确度非常依赖数据的聚簇性。

具体流程

聚类（训练阶段）

用 K-Means 将所有向量划分为 nlist 个簇。

K-Means 算法目标和数学表达

K-Means 是一种无监督聚类算法，目标是将数据划分为 k 个簇（cluster），使得：每个簇内的样本尽量相似，簇与簇之间尽量不同。 它通过最小化簇内平方误差（Within-Cluster Sum of Squares, WCSS） 来优化聚类效果。

给定数据集：

$X = x_{1}, x_{2}, \dots, x_{n}, x_{i} \in R^{d}$

我们要找到 $k$ 个质心（centroids）：

$C = c_{1}, c_{2}, \dots, c_{k}$

目标是最小化以下损失函数（簇内平方和误差，Within-Cluster Sum of Squares, WCSS）：

$J = \sum_{i = 1}^{n} {min}_{j = 1}^{k} | x_{i} - c_{j} |^{2}$

表达还是很清晰的，上述最小化损失函数翻译成人话就是：通过调整质心，使计算每个数据点到各自最近的质心的距离，再把这些距离加起来，让这个加起来距离和最小，这样质心的选择就是最精确的。 （不过因为开方运算计算量太大，而且开不开方没意义，所以这个“距离“其实是距离的平方，节省一个开方的计算量）

K-Means 算法流程

Step1 初始化中心点：
从数据集中随机选择k个点最为cluster初始质心点。

Step 2: 迭代直到收敛：

（1）分配
将各个点 $x_{i}$ 分配到各自最近的质心：
$a_{i} = \arg min_{j} | x_{i} - c_{j} |^{2}$

(2) 更新

重新计算分配数据点之后的每个中心点为其簇中所有点的均值：
$c_{j} = \frac{1}{| C_{j} |} \sum_{x_{i} \in C_{j}} x_{j}$

(3) 收敛条件

不断重复(1)(2)，直到

中心不再变化（误差变化小于阈值）
迭代次数达到上限

K-Means++

以上传统k-means算法的瓶颈则是在随机初始化中心点，很容易使最开始的中心点过于集中，从而浪费大量迭代次数于分散中心点。

于是k-means++ 用了一种更好的初始化中心点方式。

流程：
1. 随机选择第一个中心 $c_{1}$
（现在要选择第二个中心）
2. 对于每个点 x，计算其到最近中心的距离 $D (x)^{2} = min_{c} | x - c |^{2}$
3. 把每一个点的 $D (x)^{2}$ 为看作权重，构造一个概率分布：
$P (x_{i}) = \frac{D (x_{i})^{2}}{\sum_{x_{j}} D (x_{j})^{2}}$
4. 从所有点中，按这个概率分布随机选出下一个中心。即，越远越可能被选中。
（已经选择完了第二个中心）
5. 重复直到选出 k 个中心

→ 这样做可以防止所有中心点聚在一起，虽然仍然是随机，但大幅提高较远点被选为中心的概率，提高聚类稳定性和收敛速度。

举个简单例子：

假设我们有 4 个点：

点 A 距当前中心距离为 1
点 B 距离为 2
点 C 距离为 3
点 D 距离为 4

我们计算每个点的 $D (x)^{2}$ ：

点	距离 D(x)	距离平方 D(x)^2	选中概率
A	1	1	1 / 30
B	2	4	4 / 30
C	3	9	9 / 30
D	4	16	16 / 30

→ 最有可能被选为新中心的是 D，其次是 C。

构建倒排表（索引阶段）

已经构建出了k个cluster中心点，现在遍历所有数据点向量，找到其最近的中心点，加入中心点对应的cluster 倒排表中：

1
2
3

for each vector x:
    c = find_nearest_centroid(x, centroids)
    inverted_lists[c].append({id: x.id, vector: x})

每个倒排表就是一个 cluster 中的“原始向量表”。

查询流程（ANN 搜索）

搜索流程包括两个阶段：

1. 选出 nprobe 个最近中心点（coarse search）

1	nearest_centroids = top_k_by_distance(query, centroids, k=nprobe)

这一步成本是 $O (n l i s t \times (d i m + \log n p r o b e))$ ，即遍历每个中心点并计算距离。一般nprobe很小，所以成本可近似 $O (n l i s t \times d i m)$ 。但由于 nlist 通常较小（如 100~1000），速度较快。

2. 在选中的倒排表中精排（fine search）

candidates = []
for c in nearest_centroids:
    for entry in inverted_lists[c]:
        dist = distance(query, entry.vector)
        candidates.append((entry.id, dist))

return top_k(candidates)

成本为： $O (n p r o b e \times avg_list_size \times dim)$ 。

只需要在选出的少量近邻倒排表中做全量比对，即nprobe、avg_list_size都很小，故总成本远小于 brute-force。

常见参数

参数	意义	通常设置
nlist	聚类中心数量	100~1000（构建时）
nprobe	查询时探测的中心数量	1~32（运行时可调）
dim	向量维度	任意
topk	查询返回的最近邻数量	任意

实现

前面讲过的三种操作对应的API为：

/**
 * @brief Build centroids and clusters.
 */
void BuildIndex(std::vector<std::pair<std::vector<double>, RID>> initial_data) override;

/**
 * @brief The nearest "limit" number of vectors.
 */
auto ScanVectorKey(const std::vector<double> &base_vector, size_t limit) -> std::vector<RID> override;

/**
 * @brief Insert a new vector.
 */
void InsertVectorEntry(const std::vector<double> &key, RID rid) override;

而Vector Index不支持传统 Index的API

auto InsertEntry(const Tuple &key, RID rid, Transaction *transaction) -> bool override {
  UNIMPLEMENTED("call InsertVectorEntry instead");
}

void DeleteEntry(const Tuple &key, RID rid, Transaction *transaction) override {
  UNIMPLEMENTED("delete from vector index is not supported");
}

void ScanKey(const Tuple &key, std::vector<RID> *result, Transaction *transaction) override {
  UNIMPLEMENTED("call ScanVectorKey instead");
}

所以要修改 Insertion Executor，改使用向量索引对应的API。

... ...
      auto &idx_info = indexes[i];
      auto key_attri = idx_info->index_->GetKeyAttrs();

      if (key_attri.size() == 1 && schema->GetColumn(key_attri[0]).GetType() == VECTOR) {
        // Vector type, use VectorIndex API.
        auto vi = dynamic_cast<VectorIndex *>(idx_info->index_.get());
        BUSTUB_ASSERT(vi != nullptr, "Vector Key must have Vector Index.");
        auto v = new_tuple.GetValue(schema, key_attri[0]);
        vi->InsertVectorEntry(v.GetVector(), *rid);
      } else {
        // Normal index.
        auto key = new_tuple.KeyFromTuple(*schema, idx_info->key_schema_, 
          idx_info->index_->GetKeyAttrs());
        idx_info->index_->InsertEntry(key, *rid, txn);
      }
... ...

构建阶段有个小细节是，在迭代计算时，要处理当前centroid_bucket 为空的情况，我是直接不改变centroid。

先实现查找向量最近centroid 和 自动更新 centroids 的两个帮助函数：

/**
 * @brief Find the nearest centroid to the base vector in all centroids.
 * @return the nearest cnetroids index.
 */
auto FindCentroid(const Vector &vec, const std::vector<Vector> &centroids, VectorExpressionType dist_fn) -> size_t {
  BUSTUB_ASSERT(centroids.empty() == false, "centroids cannot be empty.");

  size_t nearest = -1U;
  double distance = std::numeric_limits<double>::max();

  for (size_t i = 0; i < centroids.size(); ++i) {
    auto d = ComputeDistance(vec, centroids[i], dist_fn);
    if (d < distance) {
      distance = d;
      nearest = i;
    }
  }

  return nearest;
}

/**
 * @brief Compute new centroids based on the original centroids.
 * Assign data to centroids, and re-compute new centroids.
 */
auto FindCentroids(const std::vector<std::pair<Vector, RID>> &data, const std::vector<Vector> &centroids,
                   VectorExpressionType dist_fn) -> std::vector<Vector> {
  if (data.empty()) {
    return {};
  }

  std::vector<std::vector<Vector>> centroids_buckets(centroids.size());
  for (auto &p : data) {
    centroids_buckets[FindCentroid(p.first, centroids, dist_fn)].push_back(p.first);
  }

  std::vector<Vector> new_centroids(centroids.size());
  for (size_t i = 0; i < centroids_buckets.size(); ++i) {
    auto new_centroid = VectorAvg(centroids_buckets[i]);
    new_centroids[i] = new_centroid.empty() ? centroids[i] : new_centroid;
  }
  
  return new_centroids;
}

然后就可以实现 BuildIndex:

void IVFFlatIndex::BuildIndex(std::vector<std::pair<Vector, RID>> initial_data) {
  if (initial_data.empty()) {
    return;
  }

  // Step 1: randomly initialize centroids.
  centroids_ = RandomSample(initial_data, lists_);

  // Step 2: assign and iterate. 
  for (size_t i = 0; i < build_iteration_; ++i) {
    auto new_centroids = FindCentroids(initial_data, centroids_, distance_fn_);
    
    double delta = 0.0;
    for (size_t j = 0; j < centroids_.size(); ++j) {
      delta += ComputeDistance(centroids_[j], new_centroids[j], distance_fn_);
    }
  
    centroids_ = std::move(new_centroids);
    if (delta < 1e-5) {
      break;  // convergence.
    }
  }
  
  // Step 3: put data to centroids_buckets_.
  centroids_buckets_.resize(centroids_.size());
  for (auto &p : initial_data) {
    centroids_buckets_[FindCentroid(p.first, centroids_, distance_fn_)].push_back(p);
  }
  // Shrink to save memory.
  for (auto &bucket : centroids_buckets_) {
    bucket.shrink_to_fit();
  }
}

插入新向量很简单，注意这个算法插入新向量后不需要更新centroids。

void IVFFlatIndex::InsertVectorEntry(const std::vector<double> &key, RID rid) {
  BUSTUB_ASSERT(key.size() == centroids_.front().size(), "Inserted vector has wrong dimension.");
  centroids_buckets_[FindCentroid(key, centroids_, distance_fn_)].emplace_back(key, rid);
}

接下来是查找，为了查找方便，加入一个新的帮手函数来找到最近的N个centroids:

/**
 * @brief Find the nearest N centroids.
 */
auto FindNCentroids(const Vector &vec, const std::vector<Vector> &centroids, VectorExpressionType dist_fn, 
                    size_t nprobe) -> std::vector<size_t> {
  BUSTUB_ASSERT(nprobe <= centroids.size(), "Requested centroid count exceeds available centroids.");

  std::vector<std::pair<double, size_t>> distances;
  distances.reserve(centroids.size());

  for (size_t i = 0; i < centroids.size(); ++i) {
    distances.emplace_back(ComputeDistance(vec, centroids[i], dist_fn), i);
  }

  std::partial_sort(distances.begin(), distances.begin() + nprobe, distances.end());

  std::vector<size_t> nearest_n(nprobe);
  for (size_t i = 0; i < nprobe; i++) {
    nearest_n[i] = distances[i].second;
  }
  return nearest_n;
}

继续实现查找：

auto IVFFlatIndex::ScanVectorKey(const std::vector<double> &base_vector, size_t limit) -> std::vector<RID> {
  auto nearest_centroids = FindNCentroids(base_vector, centroids_, 
    distance_fn_, probe_lists_);
    
    // Compute all distances in probe_list.
    std::vector<std::pair<double, RID>> candidates;
    for (auto c : nearest_centroids) {
      for (const auto &[v, rid] : centroids_buckets_[c]) {
        candidates.emplace_back(ComputeDistance(base_vector, v, distance_fn_), rid);
      }
    }

    size_t ans_num = std::min(limit, candidates.size());
    std::partial_sort(candidates.begin(), candidates.begin() + ans_num, 
    candidates.end(), [](const auto &a, const auto &b) { return a.first < b.first;});

    std::vector<RID> ans(ans_num);
    for (size_t i = 0; i < ans_num; ++i) {
      ans[i] = candidates[i].second;
    }
    return ans;
}

即可运行通过测试：

1 2	make -j8 sqllogictest ./bin/bustub-sqllogictest ../test/sql/vector.04-ivfflat.slt --verbose

正如之前讲的，因为IFFLAT算法只查找近邻几个cluster，为了效率牺牲了一些准确性，所以这里的测试又可能多次运行结果不一致，只要保证多组结果中有和标准答案里相同的情况，就应该是正确的实现了。

如果想更准确，可以增加构建的迭代次数，比如我从500增加到3000。但仍然会观察到结果不稳定，测试中的最后一个sql还是会偶尔出现错误的结果。虽然合理，但很难受。

接下来我改成K-means++初始化方法，把RandomSample改个名，改个实现即可：

/**
 * @brief Use K-Mean++, to randomly select "k" elements from input.
 */
auto RandomInitialCentroids(std::vector<std::pair<Vector, RID>> &input, size_t k, VectorExpressionType dist_fn) 
    -> std::vector<Vector> {
  if (k > input.size()) {
    throw std::invalid_argument("Sample size exceeds input size.");
  }

  std::unordered_map<size_t, Vector> inputs;
  size_t n = input.size();
  for (size_t i = 0; i < input.size(); ++i) {
    inputs[i] = input[i].first;
  }

  // Selecting centroids.
  std::vector<Vector> centroids;
  size_t first = rand() % n;
  centroids.push_back(inputs[first]);
  inputs.erase(first);
  k -= 1;

  std::random_device rd;
  std::mt19937 gen(rd());

  while (centroids.size() < k) {
    // Collect weights.
    std::vector<double> weights;
    std::vector<double> vectors;
    for (auto &[idx, vec] : inputs) {
      double min_dist = std::numeric_limits<double>::max();
      for (const auto &centroid : centroids) {
        double d = ComputeDistance(vec, centroid, dist_fn);
        min_dist = std::min(min_dist, d);
      }
      weights.push_back(min_dist * min_dist);
      vectors.push_back(idx);
    }
    // Random select the next centroid.
    std::discrete_distribution<> dist(weights.begin(), weights.end());
    size_t next = vectors[dist(gen)];
    centroids.push_back(inputs[next]);
    inputs.erase(next);
  }
  
  return centroids;
}

这时候再去运行测试，会发现多次尝试都可获得正确结果，不再会得到错误的测试结果，即使迭代次数只有500。可见，更准确的初始中心方法对结果的提升还是巨大的。

Hierarchical Navigable Small Worlds

在实现HNSW之前，先实现一个基本组件 **NSW (Navigable Small Worlds)**。

介绍

这个算法维护图中节点与近邻之间的连接，查找时从一个节点开始，不断判断其相邻节点是否与目标节点更近，并持续跳向更近的节点，直到找不到更近的节点。

请添加图片描述
如图，查找距离蓝色节点最近的节点，先随机从Entry Point 开始，计算其相邻节点是否更近，然后跳转到更近的1st节点，再同样的方式跳转到2nd节点，此时发现四周节点都更远，说明找到最近节点。

而构建则是类似，先查找最近邻的M个节点，然后插入并将最近邻的M个节点相连。

这个算法查找速度和内存消耗都大于IFFlat，但提升了查找精度以及可以动态构建。当然，这中贪心算法也有很大的缺点，也就是很容易陷于局部最优，很依赖图构建的质量和初始点的选取。

也有解决局部最优的几个思路：

多起点搜索（multi-entry search）：从多个随机点开始，多次贪心搜索，取最优。
beam search / best-first search：维护一个候选集合而非单一节点，跳更稳。
随机跳跃：加入一些概率性非贪心跳跃（如 Simulated Annealing 思想）。

而这里我们也用了多起点搜索和priority-queue。

实现

我们的实现用了多起点➕best-first search。

需要维护两个数据结构，一个priority-queue存放候选节点，记为C；一个binary-heap存放最近的k个结果，记为W。

请添加图片描述
如上图，初始状态，将两个入口节点放入候选队列C和结果集合W。
从候选队列pop出下一个节点，即红色节点，遍历其邻居节点，计算距离，加入候选节点队列C和结果集合W。而结果集合只保留最近的k个节点。

再继续从候选集合C中pop节点，直到所有候选节点的距离都要远于结构集合里节点的距离。（注意要避免将已经遍历过的节点重复加入候选合集）

auto NSW::RandomSample(size_t ef_construction) -> std::vector<size_t> {
  auto vertice = in_vertices_;
  std::random_device rd;
  std::shuffle(vertice.begin(), vertice.end(), rd);

  size_t sample_size = std::min(ef_construction, vertice.size());
  return {vertice.begin(), vertice.begin() + sample_size};
}

auto NSW::Insert(const std::vector<double> &vec, size_t vertex_id, size_t ef_construction, size_t m) {
  auto entries = RandomSample(ef_construction);
  auto nearest = SearchLayer(vec, m, entries);

  AddVertex(vertex_id);

  for (size_t x : nearest) {
    auto &lists = edges_[x];
    if (lists.size() == m_max_) {
      auto it = std::max_element(
        lists.begin(), lists.end(),
        [&](size_t a, size_t b) {
          return ComputeDistance(vertices_[x], vertices_[a], dist_fn_) <
                 ComputeDistance(vertices_[x], vertices_[b], dist_fn_);
        });
      auto removed = *it;
      lists.erase(it);
      auto &rev_list = edges_[removed];
      rev_list.erase(std::remove(rev_list.begin(), rev_list.end(), x), rev_list.end());
    }
    Connect(vertex_id, x);
  }
}

运行测试会发现还是有不稳定的问题，有时候能返回正确结果，有时候返回错误结果。

解决局部最优最有效实用的方法还是HNSW，也是现在现代向量数据库如pgvector之类最主流的方法。

Hierarchical Navigable Small World

这部分则会基于NSW，实现Hierarchical Navigable Small World（层次化可导航小世界图） 的一种高效向量近似最近邻搜索（ANN） 算法。

请添加图片描述

思路

这里基于Intuition介绍一下，其通过构建多层次的图结构来加速向量检索，即一堆向量建一个多层的“跳跃网络”。核心思路是：

分层组织：将向量点随机划分到不同的层级。层数高的节点越稀疏节点之间距离远，用于快速远距离跳跃；层级低的节点越密集节点之间距离近，用于具体定位到精确节点。
近邻连接：在同一层，节点只连自己附近的点。并有少量的随机远距离连接。
层次导航：
- 在上层图中，节点稀疏且连接长距离，可以快速跳跃，找到查询向量的大致方向。
- 在下层图中，节点密集且连接近邻，可以细致搜索，找到精确的最近邻。

整体上，HNSW结合了局部聚集性（找到最近邻）和全局跳跃性（快速定位）两种特性，使得在海量向量数据中，也能用极少的跳跃快速找到目标。这种设计与跳表（Skip List） 非常相似。

玩过《都市天际线》应该很容易理解，HNSW的结构和城市路网很类似。

在城市中，建筑往往聚集成簇，比如住宅区、商业区、工业区。每个簇内部建筑密集，但簇与簇之间距离较远，整体呈现出一种局部密集、整体稀疏的结构。

如果使用最naive的“格子城”设计——所有道路宽度相同、网格均匀排布——那么远距离通行时，车辆需要经过大量路口，频繁停车等待，通行效率极低。而这就相当于NSW，当搜索初始节点和目标节点相距很远的时候，就要经过大量的“路口”才能找到最近节点，这大大降低了效率。

为了解决这个问题，城市路网设计引入了道路分级。比如，从居民区到工业区，会设计一条宽阔的高速路，通过尽量少的路口直达目的地；而到了工业区附近，再通过高速辅路下高速，进入工业区内部密集的小街道。这些小街道虽然路口密集、易堵车，但因为它们属于末端道路，不会影响城市高速主干道的整体通行效率。

HNSW的设计正是如此。
高速公路、辅路、密集小路，分别对应HNSW中从上到下的不同层级：

高层（高速路）：快速跳跃，减少跳转次数，快速接近目标区域。
中层（辅路）：过渡连接，定位更精确的子区域。
低层（小街道）：局部密集搜索，最终精准找到最近的节点。

高级层级负责远距离快速定位，低级层级负责细粒度的精确查找。这就是HNSW结构与城市路网惊人相似之处。

现在举个例子，比如数据库里有这些向量：[1] [2] [3] [10] [11] [12] [50] [51] [52]

如果你查11附近的点，暴力法要每个都算一遍距离，超级慢。

但HNSW是：

先在高层，从比如50出发
发现11比50近，就跳到10
10周围是11、12，一下子找到最近的邻居！

跳几步就搞定了！而不是扫一遍。

（假设2层图）

1
2
3

1 ----- 10 ---- 50                   Level 1     远距离连接，通行更快
 \             /
  2----3----11----12----51----52     Level 0     更密集连接，能走得更细

Level 1用于快速粗定位，Level 0用于精细局部搜索，很类似跳表。

实现

HNSW 的每一层相当于一个NSW。

查找

查找时从高层开始，向底层查找。
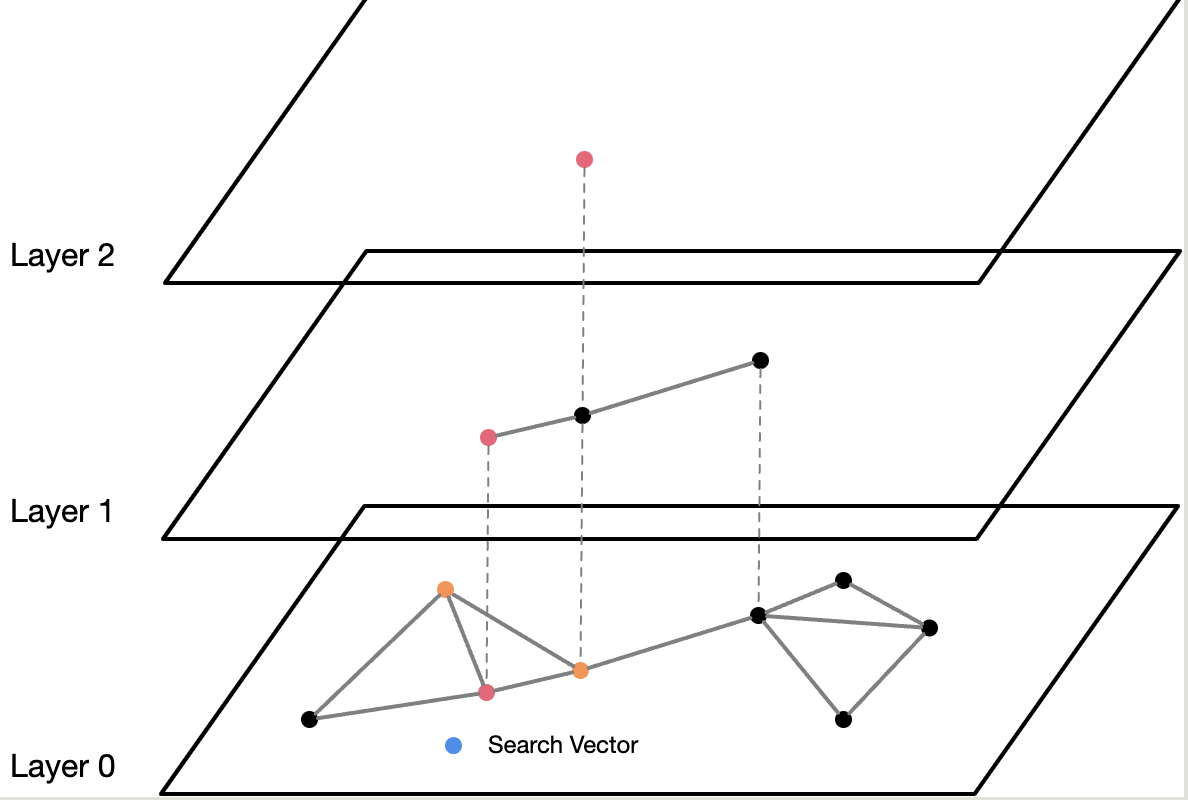
请添加图片描述

如图，先从 Layer 2 开始，找到最近邻节点后，以其为起始点，下到 Layer 1 继续查找最近邻点，找到后再进入 Layer 0 也就是最底层，查到最近邻的k个点。

重要的一点是，高层搜索时要用eof_search 作为搜索宽度，然后再用SearchNeighbor() 找出最近的节点，因为这样才能保持一个较宽的搜索宽度，使搜索更精确。

插入

插入节点首先必定要插入底层（类似跳表），因为底层要维护所有节点。并且根据一定的概率来判断是否要插入上层节点，插入层数遵循这样的公式：

$level = ⌊ - \ln (unif (0, 1)) \times m_{L} ⌋$

$unif (0, 1)$ 是一个 $[0, 1)$ 的随机均匀分布。

外层加一个 $- \ln$ 取其对数，其概率密度分布变成了 $f (x) = e^{- x}$ ，即大的数概率小，小的数概率大。这样就相当于高层建新节点的概率呈指数级下降。

$m_{L}$ 是一个可调参数。

最后再向下取整。

代码

查找最近邻：

auto SelectNeighbors(const std::vector<double> &vec, const std::vector<size_t> &vertex_ids,
  const std::vector<std::vector<double>> &vertices, size_t m, VectorExpressionType dist_fn) -> std::vector<size_t> {
  std::vector<std::pair<double, size_t>> distances;
  distances.reserve(vertex_ids.size());

  for (const auto vert : vertex_ids) {
    distances.emplace_back(ComputeDistance(vertices[vert], vec, dist_fn), vert);
  }

  std::sort(distances.begin(), distances.end());
  std::vector<size_t> selected_vs;
  selected_vs.reserve(vertex_ids.size());

  for (size_t i = 0; i < m && i < distances.size(); i++) {
    selected_vs.emplace_back(distances[i].second);
  }

  return selected_vs;
}

搜索：

auto HNSWIndex::ScanVectorKey(const std::vector<double> &base_vector, size_t limit) -> std::vector<RID> {
  std::vector<size_t> vertex_ids;

  // Traverse layers.
  for (int l_idx = layers_.size() - 1; l_idx >= 1; l_idx--) {
    NSW &layer = layers_[l_idx];
    if (vertex_ids.empty()) {
      vertex_ids = layer.SearchLayer(base_vector, ef_search_, layer.RandomSample(1, generator_));
    } else {
      vertex_ids = layer.SearchLayer(base_vector, ef_search_, vertex_ids);
    }
    vertex_ids = SelectNeighbors(base_vector, vertex_ids, *vertices_, 1, distance_fn_);
  }

  // Bottom layer.
  vertex_ids = layers_[0].SearchLayer(base_vector, limit > ef_search_ ? limit : ef_search_, vertex_ids);
  vertex_ids = SelectNeighbors(base_vector, vertex_ids, *vertices_, limit, distance_fn_);

  std::vector<RID> result;
  result.reserve(vertex_ids.size());
  for (size_t i = 0; i < std::min(limit, vertex_ids.size()); ++i) {
    result.push_back(rids_[vertex_ids[i]]);
  }
  return result;
}

插入新节点：

void HNSWIndex::InsertVectorEntry(const std::vector<double> &key, RID rid) {
  auto id = AddVertex(key, rid);

  size_t level = RandomLevel();
  while (layers_.size() <= level) {
    layers_.emplace_back(*vertices_, distance_fn_, m_max_);
  }
  
  // Traverse to level + 1.
  std::vector<size_t> vertex_ids;
  for (int l_idx = layers_.size() - 1; l_idx > static_cast<int>(level); l_idx--) {
    NSW &layer = layers_[l_idx];
    if (vertex_ids.empty()) {
      vertex_ids = layer.SearchLayer(key, 1, layer.RandomSample(1, generator_));
    } else {
      vertex_ids = layer.SearchLayer(key, 1, vertex_ids);
    }
    vertex_ids = SelectNeighbors(key, vertex_ids, *vertices_, 1, distance_fn_);
  }

  // Insert to layer.
  for (int l_idx = level; l_idx >= 0; l_idx--) {
    NSW &layer = layers_[l_idx];
    if (vertex_ids.empty()) {
      vertex_ids = layer.RandomSample(1, generator_);
    }
    layer.Insert(key, id, ef_construction_, m_, vertex_ids);
  }
}

auto HNSWIndex::RandomLevel() -> size_t {
  std::uniform_real_distribution<double> distrib(0.0, 1.0);
  double u = distrib(generator_);
  int level = static_cast<int>(std::floor(-std::log(u) * m_l_));
  return level;
}

即可通过测试。

整体来说如果做过Project 3 leaderboard部分，就不算难，几个三种向量索引如果理解了，实现也是很简单，但原版讲义还是有很多可以优化的部分。